Analyzing single-cell RNA-seq perturbation with DECAL

André M. Ribeiro-dos-Santos

11/18/2021

Abstract

Single-cell RNA sequencing technology has allow us to explore cell specific expression patterns. Functional genomics have been exploring such dataset to establish direct link between genetic alterations and differential gene expression. The package DECAL (Differential Expression analysis of Clonal Alterations Local effects) provides tools to explore single-cell of perturbed cells populations. It uses a negative binomial generalized linear model to evaluate gene expression changes between clonal cell populations and gene candidates. The present vignette explains the package usage, demonstrantes a typical analysis workflow, and explains the package statistical model. decal package version: 0.1.1

Default Workflow

DECAL (Differential Expression analysis of Clonal Alterations Local effects) provide you with tools to conduct differential expression analysis of single-cell perturbations experiments to potentially interacting genes. Similar to other differential expression analysis tools, it models gene expression using a Negative Binomial (or Gamma-Poisson) regression, modeling each gene UMI count by the cell alteration status and cell total count.

Features

• decal is compatible with tidyverse analysis.
• Includes a suit of simulation functions to generate your own dataset based decal model and evaluate your statistical power.
• Package has few dependencies, requiring only MASS, fastglm and Matrix.
• Can evaluate specific clonal alteration and gene effect, instead of modeling all genes and all alterations. This allow us to quickly investigate a large number of interactions skipping unlikely effects.

Installation

To install decal package current version, open your R terminal and type:

## Install remotes if not available with
## install.install.packages("remotes")
remotes::install_github("mauranolab/decal")

Using decal

The package main function (decal) runs the whole statistical analysis by fitting a Negative Binomial (or Gamma-Poisson) regression to each gene and alteration pair specified and evaluate the perturbation statistical significance for a single-cell perturbation experiment. You can run decal as follow:

decal(perturbations, count, clone)

The three parameters required are the following:

• a table specifying the population and gene to evaluate perturbation (perturbations).
• a UMI count matrix that each column correspond to a cell and each row a gene or feature (count).
• a list of cells specifying your clones composition (clone). This is represented by a R list composed by character (or integer) vectors named after the clone ID and indicating the cells belonging to this clone.

decal returns a deep copy of the perturbations table with the following additional columns:

• n0 and n1: number of non-perturbed and perturbed cells, respectively.
• x0 and x1: average UMI count among perturbed and non-perturbed cells, respectively.
• mu: average UMI count among all cells.
• xb: expected average UMI count of perturbed cells.
• theta: estimated negative binomial dispersion parameter.
• z: estimated perturbation z-score.
• lfc: log2 fold-change of perturbed cells gene expression.
• pvalue and p_adjusted: perturbation t-test significance values.

Quick Start

Below we include a example of decal analysis on a simulated dataset included with our package.

library(decal)

data("sim_decal")
perturbations <- sim_decal$perturbations
count <- sim_decal$count
clone <- sim_decal$clone

res <- decal(perturbations, count, clone)
head(res)

clone	gene	expected_lfc	n0	n1	x0	x1	mu	theta	xb	z	lfc	pvalue	p_adjusted
clone-001	gene1353	0	979	21	57.3	60.0	57.4	78	60.2	1.30	0.07	0.20	0.31
clone-001	gene1212	0	979	21	37.3	38.0	37.3	73	38.4	0.63	0.04	0.53	0.69
clone-001	gene1032	0	979	21	21.6	21.9	21.6	76	22.2	0.46	0.04	0.65	0.77
clone-001	gene504	0	979	21	4.3	4.2	4.3	46	4.3	-0.03	0.00	0.98	0.98
clone-001	gene1065	0	979	21	23.9	22.8	23.9	75	22.8	-0.87	-0.07	0.38	0.54
clone-001	gene995	0	979	21	19.4	19.7	19.4	77	19.8	0.37	0.03	0.71	0.82

Exploring decal results

Now let’s explore decal results. Admitting a 5% false discovery rate (FDR), we can select significantly differentiate perturbations by picking those with p_adjusted < 0.05. Below we present the top 5 interactions with highest reducing and increasing log fold-change effect (as measured by lfc).

sig <- subset(res, p_adjusted < 0.05)
sig <- sig[order(sig$lfc), ]
## select first 5 and last 5 since`sig` is ordered by lfc
pick <- c(1:5, nrow(sig) - 1:5)
sig[pick,]

	clone	gene	expected_lfc	n0	n1	x0	x1	mu	theta	xb	z	lfc	pvalue	p_adjusted
352	clone-008	gene130	-3	972	28	1.4	0.04	1.4	18	0.03	-3.7	-5.4	0.00	0.00
83	clone-002	gene094	-2	986	14	1.2	0.07	1.2	17	0.08	-2.7	-3.9	0.01	0.01
572	clone-013	gene265	-3	970	30	2.0	0.13	1.9	22	0.13	-5.7	-3.9	0.00	0.00
483	clone-011	gene993	-3	995	5	19.8	1.20	19.7	77	1.41	-5.7	-3.8	0.00	0.00
88	clone-002	gene790	-3	986	14	10.1	0.71	10.0	68	0.82	-8.0	-3.6	0.00	0.00
471	clone-011	gene1207	3	995	5	37.4	264.40	38.5	73	313.85	22.9	3.1	0.00	0.00
648	clone-015	gene1069	3	979	21	24.0	194.24	27.6	73	199.02	69.8	3.0	0.00	0.00
604	clone-014	gene636	3	992	8	6.4	52.62	6.8	61	52.89	30.2	3.0	0.00	0.00
120	clone-003	gene699	3	981	19	7.5	69.47	8.7	67	62.17	51.5	3.0	0.00	0.00
76	clone-002	gene150	3	986	14	1.5	10.50	1.6	19	12.08	20.6	3.0	0.00	0.00

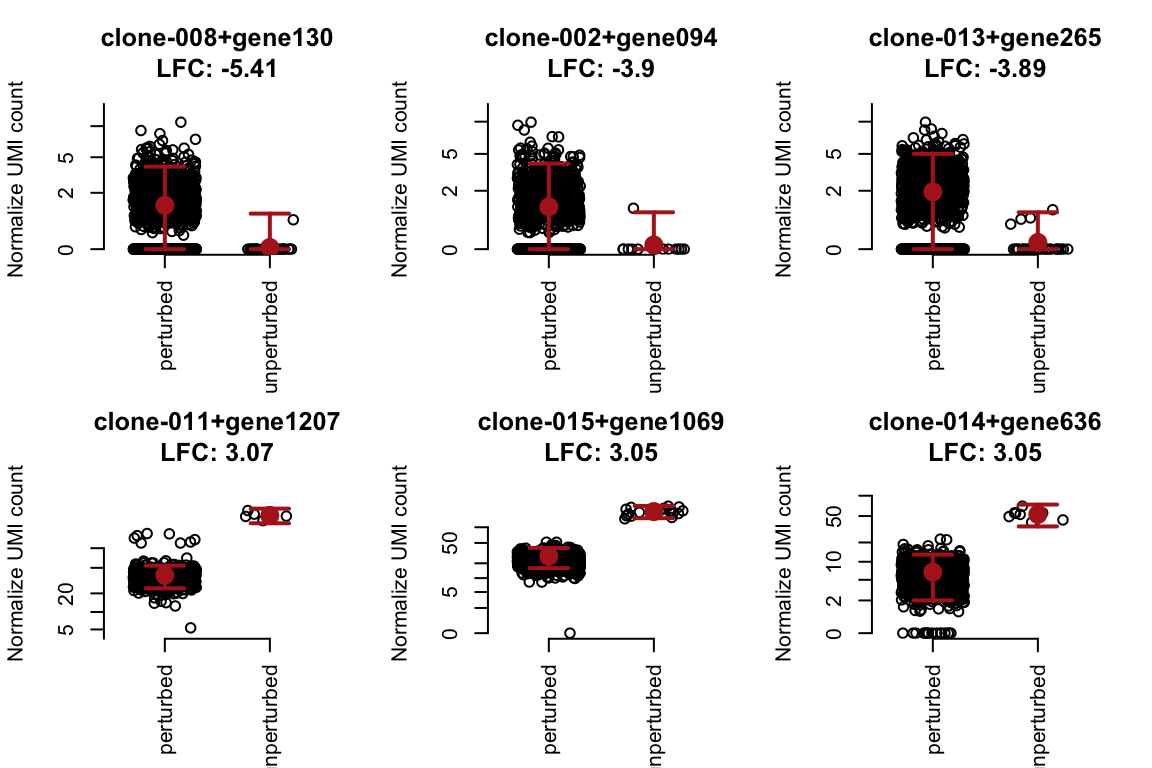
To visualize the perturbation effect, let’s plot the top 3 interactions increasing and reducing gene expression.

## compute a normalize size-factor
sf <- mean(colSums(count)) / colSums(count)
## add log10(x+1) transformation function
log10p <- function(x) log10(x + 1)

## pick tables first 3 and last 3
pick <- c(1:3, nrow(sig) - 1:3)

par(mfrow = c(2, 3))
for (i in pick) {
  ## Determinate perturbed and unperturbed cells
  x <- colnames(count) %in% clone[[sig$clone[i]]]
  ## Calculate normalized expression count
  y <- count[sig$gene[i],] * sf
  ## plot jitter
  title <- paste0(sig$clone[i], "+", sig$gene[i],"\nLFC: ", round(sig$lfc[i], 2))
  plot(
    x + runif(length(x), -.3, .3), log10p(y), main = title,
    axes = FALSE, xlab = "", ylab = "Normalize UMI count",
    xlim = c(-.5, 1.5), ylim = c(0.9, 1.1) * range(log10p(y))
  )
  axis(1, at = 0:1, labels = c("perturbed", "unperturbed"), las = 2)
  axis(2, at = log10p(c(0, 2, 5, 10, 20, 50, 100)), labels = c(0, 2, 5, 10, 20, 50, 100))
  ## add 95% error bar
  ymed <- c(sig$mu[i], sig$xb[i])
  ylow <- qnbinom(0.025, size = sig$theta[i], mu = ymed)
  yupr <- qnbinom(0.975, size = sig$theta[i], mu = ymed)
  points(c(0, 1), log10p(ymed), col = "firebrick", cex = 2, pch = 16)
  arrows(
    x0 = c(0, 1), y0 = log10p(ylow), x1 = c(0, 1), y1 = log10p(yupr),
    code = 3, angle = 90, col = "firebrick", length = .1, lwd = 2
  )
}

Evaluating decal results

In our sim_decal simulated dataset, we introduced some real expression perturbations as indicated by expected_lfc column in perturbations table, such as a 0 expected_lfc indicate no change was applied. We can evaluate our results using the confusion matrix below:

conf_mat <- table(real = res$expected_lfc != 0, decal = res$p_adjusted < 0.05)
round(prop.table(conf_mat), 3)
#>        decal
#> real    FALSE  TRUE
#>   FALSE 0.447 0.009
#>   TRUE  0.026 0.518

Based on this confusion matrix, our decal model presented:

• Accuracy: 0.96
• Precision: 0.95
• Recall: 0.98
• F1 Score: 0.97
• Observed FDR: 0.04

These results show great metrics with recall, accuracy, precision and F1 score above 95% and a false discovery ratio within our admitted 5%.

Next, let’s explore how well decal estimated the real log2 fold-change (LFC) applied. Illustrated below is the decal estimated LFC (lfc column in res) distribution for each of the real perturbations values applied (expected_lfc column).

lfc_histogram <- function(lfc, fn = function(x) { x$count / sum(x$count) }) {
  hist_breaks <- c(-Inf, seq(-4, 4, length.out = 50), Inf)
  hist_counts <- lapply(lfc, hist, breaks = hist_breaks, plot = FALSE)
  hist_ymax <- max(sapply(hist_counts, fn))
  plot(c(-4, 4), c(0, hist_ymax), type = "n",
    xlab = "Estimated LFC", ylab = "Proportion of interactions")
  for(i in seq_along(hist_counts)) {
    lines(hist_counts[[i]]$mids, fn(hist_counts[[i]]), col = i, type = "s")
  }
  legend("topleft", title = "Real LFC", legend = names(hist_counts),
    col = seq_along(hist_counts), bty = "n", lty = 1, lwd = 2, ncol = 2)
}

lfc_histogram(split(res$lfc, res$expected_lfc))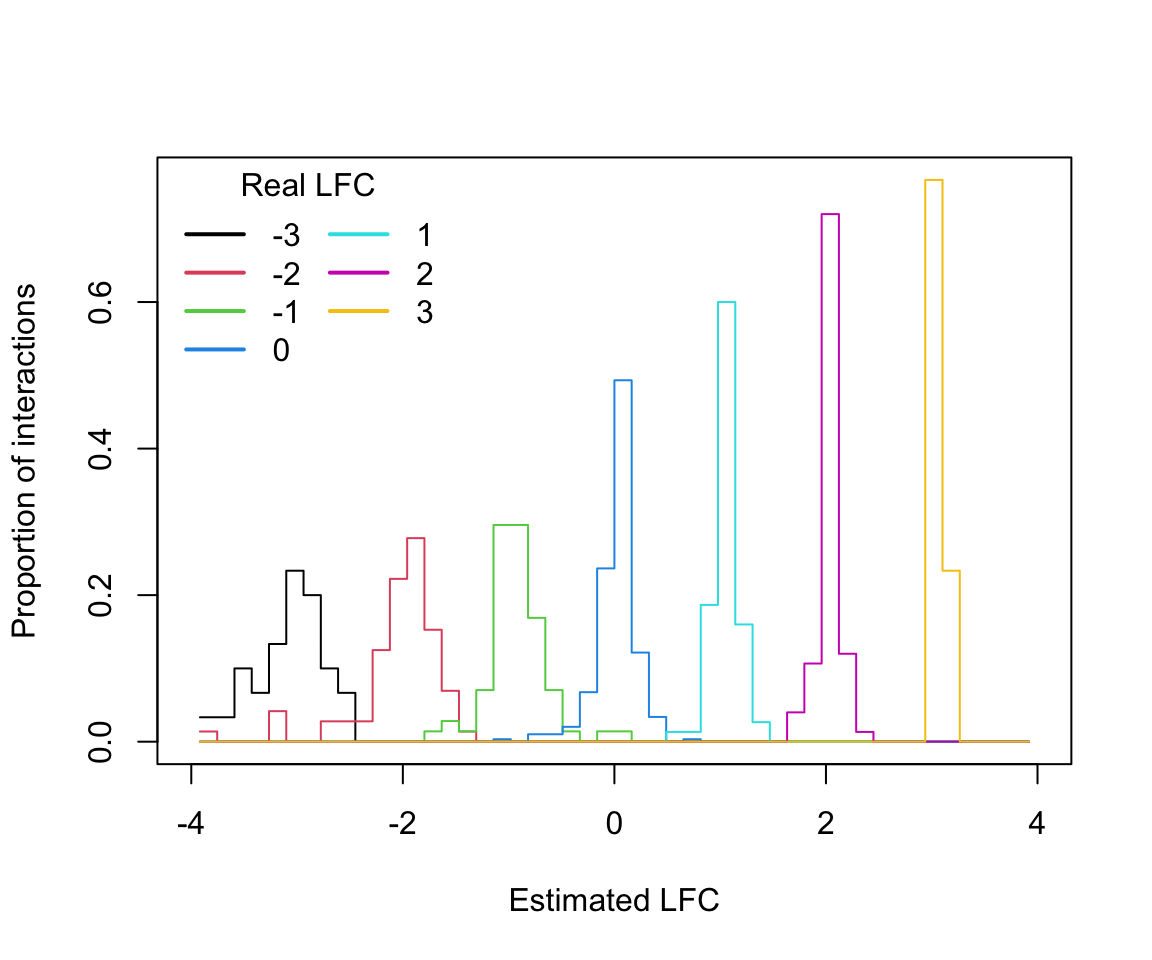

Finally, we can measure decal LFC estimative Mean Squared Error (MSE) and Rooted MSE (RMSE) using the code below. The results indicate that decal estimates presented high accuracy and precision with RMSE below 1 LFC for all perturbations effects applied.

err <- (res$lfc - res$expected_lfc)**2
err <- split(err, res$expected_lfc)
mse <- sapply(err, mean, na.rm = TRUE)

data.frame(
  N = sapply(err, length),
  MSE = mse, RMSE = sqrt(mse)
)

	N	MSE	RMSE
-3	30	0.31	0.56
-2	75	0.19	0.43
-1	75	0.08	0.27
0	300	0.04	0.21
1	75	0.02	0.13
2	75	0.01	0.11
3	30	0.00	0.05

Exploring decal arguments

As mentioned before, decal function requires three main parameters:

1. perturbation, a table specifying the clone population and gene to evaluate differential expression.
2. count, a UMI count matrix where each column correspond to a cell and each row a gene or feature.
3. clone, a list of cells specifying each clone populations composition.

In the next sections, we will further illustrate and give alternative formats for (1) and (3).

Electing potential gene perturbations

Since decal was designed to explore specific gene perturbations, it requires you to specify clone and gene (or features) pairs to evaluate expression change among the cells within the clone in regards to all other cells. For example, in our original study after we localized our alternations and evaluated their impact to all genes within 250 kbp.

In sim_decal$perturbations data.frame (see snippet below) the clone and gene pairs are specified by the clone and gene columns, which can be an id (as character vector) or index (as integer vector). In the case these elements are specified as an index, they identify the ith element of sim_decal$clone and row position in sim_decal$count, respectively.

head(sim_decal$perturbations)

clone	gene	expected_lfc
clone-001	gene1353	0
clone-001	gene1212	0
clone-001	gene1032	0
clone-001	gene504	0
clone-001	gene1065	0
clone-001	gene995	0

By default decal uses the clone and gene columns, but you can specify a different column using gene_col and clone_col parameters like in the example below.

alt_pert <- data.frame(gene_ix = 101:110, clone_ix = 1:10)
decal(alt_pert, count, clone,
  gene_col = "gene_ix", clone_col = "clone_ix")

	gene_ix	clone_ix	n0	n1	x0	x1	mu	theta	xb	z	lfc	pvalue	p_adjusted
clone-001	101	1	979	21	1.3	1.05	1.2	17	1.06	-0.78	-0.25	0.43	0.87
clone-002	102	2	986	14	1.2	1.00	1.2	17	1.15	-0.29	-0.11	0.77	0.98
clone-003	103	3	981	19	1.2	1.42	1.2	17	1.23	-0.04	-0.01	0.97	0.98
clone-004	104	4	981	19	1.2	1.11	1.2	17	1.04	-0.81	-0.25	0.42	0.87
clone-005	105	5	976	24	1.2	1.58	1.2	17	1.57	1.49	0.37	0.14	0.66
clone-006	106	6	993	7	1.2	1.00	1.2	17	1.37	0.28	0.15	0.78	0.98
clone-007	107	7	989	11	1.3	0.73	1.3	18	0.81	-1.29	-0.68	0.20	0.66
clone-008	108	8	972	28	1.2	1.79	1.3	17	1.64	1.87	0.39	0.06	0.62
clone-009	109	9	979	21	1.3	1.38	1.3	18	1.34	0.02	0.01	0.98	0.98
clone-010	110	10	975	25	1.3	1.40	1.3	18	1.26	-0.22	-0.06	0.82	0.98

Defining your experiment clonal structure

After identifying your cells’ clonal populations you can specify it decal (clone parameter) as a R list where each element is clone represented by a collection of ids (as character vector) or index (as integer vector) indicating the set of cells belonging to the clone. When the cells are specified by index, they correspond to the column position in your count matrix. See below a example from sim_decal$clone

sim_decal$clone[1:2]
#> $`clone-001`
#>  [1] "cell998" "cell741" "cell558" "cell339" "cell085" "cell701" "cell096"
#>  [8] "cell843" "cell477" "cell410" "cell675" "cell379" "cell323" "cell620"
#> [15] "cell232" "cell213" "cell830" "cell676" "cell117" "cell784" "cell352"
#> 
#> $`clone-002`
#>  [1] "cell438" "cell443" "cell464" "cell420" "cell922" "cell424" "cell704"
#>  [8] "cell149" "cell665" "cell214" "cell569" "cell444" "cell315" "cell955"

Reducing noise and increasing power

To improve your findings, decal includes some filtering arguments to avoid testing interactions with low statistical power:

• min_x: minimal average UMI count on perturbed and unperturbed cells (indicated by x1 and x0 on resulting table, respectively).
• min_n: minimal number of perturbed cells (indicated by n1).
• min_mu: minimal global average count (indicated by mu), also skips theta estimation.

Interactions that doesn’t met all of these requirements are skipped and no differential expression analysis is conducted, eventhough they are no removed from the results. By default, decal applies the following minimal filters min_x = 1; min_n = 2; and min_mu = 0.05.

Understanding decal model

Statistical model

The decal statistical model is based on the observations that UMI counts of a particular gene approximates a Poisson or Negative Binomial distribution in a single-cell RNA-seq experiment (Svensson 2020; Townes et al. 2019). Thus, we proposed to model the observed counts as follow:

\[ Y_{gc} \sim NB(\mu_{gci}, \theta_g) \tag{1} \]

where \(Y_{cg}\) is the UMI count for gene g and cell c modeled using a negative binomial distribution with expected count \(\mu_{cgi}\) and a gene-specific dispersion parameter \(\theta_g\).

\[ log(\mu_{gci}) = log(D_c) + \beta_g + \beta_x X_{ci} \tag{2} \]

The \(log(\mu_{cgi})\) (or log expected count) is proportional to the perturbation effect (\(\beta_x\)) of a specific clone i indicated by \(X_{ci}\) (where \(X_{ci} == 1\) if cell c belongs to the perturbed clone or \(X_{ci} == 0\) otherwise) and offseted by the log cell total UMI count (\(D_c = \sum_g Y_{cg}\)).

The parameter \(\theta_g\) defines the model dispersion where smaller values produce a wider distribution and higher values produce a tighter distribution that coincides with a Poisson distribution. Such as the model variance is defined as follow:

\[ \begin{aligned} Var(Y_{cg}) & = E[(Y_{cg} - \mu_{cgi})^2] \\ & = \mu_{cgi} + \mu_{cgi}^2/\theta_g \\ \lim_{\theta\to\infty} NB(\mu, \theta) & = Pois(\mu) \end{aligned} \tag{3} \]

This modeling approach is similar to previously published models such as edgeR (Robinson, McCarthy, and Smyth 2010; McCarthy, Chen, and Smyth 2012), DESeq2 (Anders and Huber 2010; Love, Huber, and Anders 2014), and glmGamPoi (Ahlmann-Eltze and Huber 2021). But it differs in two points: (i) to estimate \(\theta_g\) we adopted a regularized estimation strategy to make it robust to sampling noise in low expression genes; and (ii) instead of fitting the model to all genes, it fits and measure specific perturbation to gene.

Estimating dispersion

To estimate and regularize our \(\theta_g\), we adopted the strategy described by Hafemeister and Satija (2019). This strategy consists in first selecting about 2000 genes, estimating their expect count (\(mu_{cg}\)) using a naive Poisson regression offseted by the log cell total count, such as:

\[ \begin{aligned} Y_{cg} & \sim Pois(mu_{cg}) \\ log(mu_{cg}) & = \beta_g + log(D_c) \end{aligned} \tag{4} \]

Next, we use \(mu_{cg}\) to make a naive estimate of \(\theta_g\) using a maximum likelihood estimator (MASS::theta_ml function). The resulting naive estimate was finally regularized by fitting it to a kernel smooth regression as a function of the average gene count (\(\sum_g Y_{cg} / N\)) to produce our final estimate of \(\theta_g\). Illustrate below is a scatterplot of each naive estimate, in red our final regularized estimate and in black the real dispersion applied when simulating sim_decal dataset.

raw_theta <- attr(res, "raw_theta")
mu <- rowMeans(count)
mu_breaks <- c(0.01, 0.1, 1, 2, 5, 10, 20, 50, 100)

plot(log10(mu), raw_theta,
  xlab = "Average expression (mu)", xaxt = "n",
  ylab = expression(theta), ylim = c(0, 150))
abline(h = 100)
lines(log10(res$mu[order(res$mu)]), res$theta[order(res$mu)], col = 2, lwd = 3)
axis(1, at = log10(mu_breaks), labels = mu_breaks)
legend(
  "topleft", c("Naive Estimate", "Regularized Estimate", "Real"),
  pch = c(1, NA, NA), lty = c(NA, 1, 1), col = c(1, 2, 1)
)

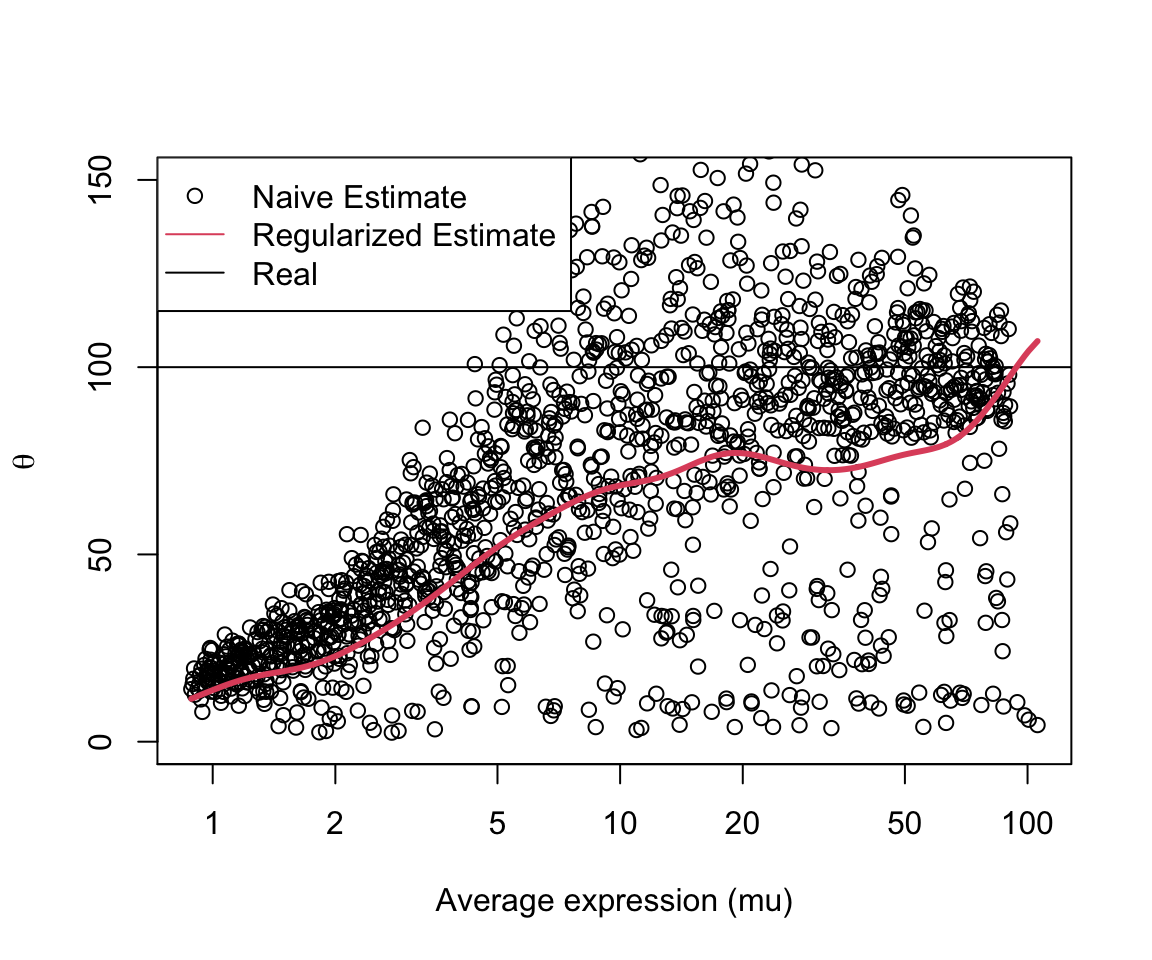
As shown above, our regularized estimates approximates the real dispersion values and control some of the excessive fluctuation presented by our naive estimate.

Assumptions and Caveats

It is worth notice that decal statiscal model implies some assumptions and caveats:

1. The UMI count distribution is independent between genes, which is usually true for single-cell experiments due to large quantity of genes and small proportion of counts each of them represent.
2. The effect of individual clones are not enough to affect the unperturbed estimates for other clones. For such assumption to hold, the number of perturbated cells of any clone must be much smaller than the total number of cells available (n1 << N). This allow us to explore each clone independently, since it makes the effect of other clones to our unperturbed estimates negletable.
3. The cells investigates must represent an uniform population differing only by the induced alterations. This can safely be assumed when the experiment is conducted in a uniform cell culture.

Simulating

Since many factor can affect your experiment, we included to decal a way to simulate a dataset under our model assumptions (see equation (1)). These tools will allow you to estimate your experiment power and sensitivity under different conditions you may find.

decal simulation suite is compose of various functions to generate a count matrix (sim_count and sim_count_from_data), randomly assign cells to different clones (sim_clone and sim_clone_range), and generate a full experiment dataset (sim_experiment and sim_experiment_from_data). Here we will use sim_experiment and sim_experiment_from_data to generate our examples, but the other functions behave similarly.

Evaluating our model under null hypothesis

Under the null hypothesis, we expect that our perturbations produce no expression change to nearby genes. Admitting a FDR of 5% and that decal statistical model holds, we would expect that the resulting z-score present a normal distribution centered at 0, p-value have a uniform distribution and about 5% of the tests below our significance threshold.

Given an existing dataset, we can evaluate if our model holds by randomly recombining clone and gene pairs.

rnd <- unique(data.frame(
  clone = sample(perturbations$clone),
  gene = sample(perturbations$gene)
))
## remove previous clone + gene pairs
rnd <- rnd[!paste(rnd$gene, rnd$clone) %in% paste(perturbations$gene, perturbations$clone),]
rnd_res <- decal(rnd, count, clone)
rnd_res <- subset(rnd_res, !is.na(rnd_res$pvalue))

par(mfrow = c(1, 3))
hist(rnd_res$z, xlab = "Z-score", main = "")
hist(rnd_res$pvalue, xlab = "Observed Pvalue", main = "")
hist(rnd_res$p_adjusted, xlab = "Observed Qvalue", main = "")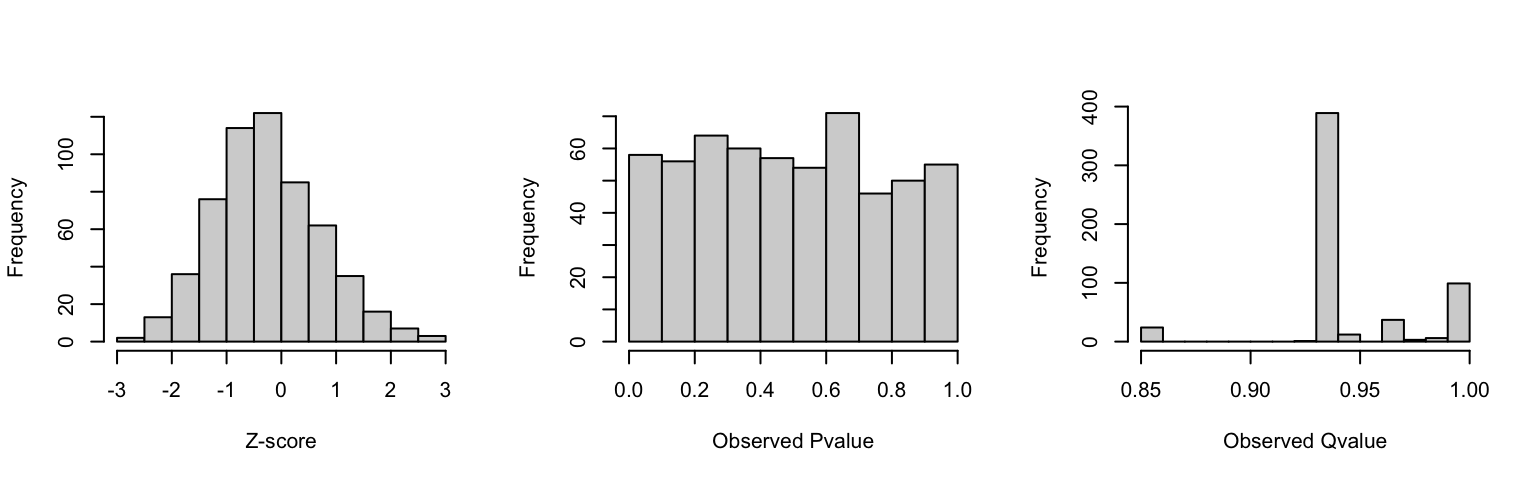

mean(rnd_res$pvalue < 0.05)
#> [1] 0.046
mean(rnd_res$p_adjusted < 0.05)
#> [1] 0

As expected, this experiment z-score presented the expected z-score and p-value distribution and the ratio of tests with p-value below the significance threshold (0.05) within the expected 5% at random.

We can conduct a similar experiment producing a random count matrix based on your experiment counts. sim_count_from_data will simulate a UMI count matrix with the same dimensions as your experiment with cells total UMI count and gene average expression similar to your reference count matrix.

rnd_count <- sim_count_from_data(count)

rnd_res <- decal(perturbations, rnd_count, clone)
rnd_res <- subset(rnd_res, !is.na(rnd_res$pvalue))

par(mfrow = c(1, 3))
hist(rnd_res$z, xlab = "Z-score", main = "")
hist(rnd_res$pvalue, xlab = "Observed Pvalue", main = "")
hist(rnd_res$p_adjusted, xlab = "Observed Qvalue", main = "")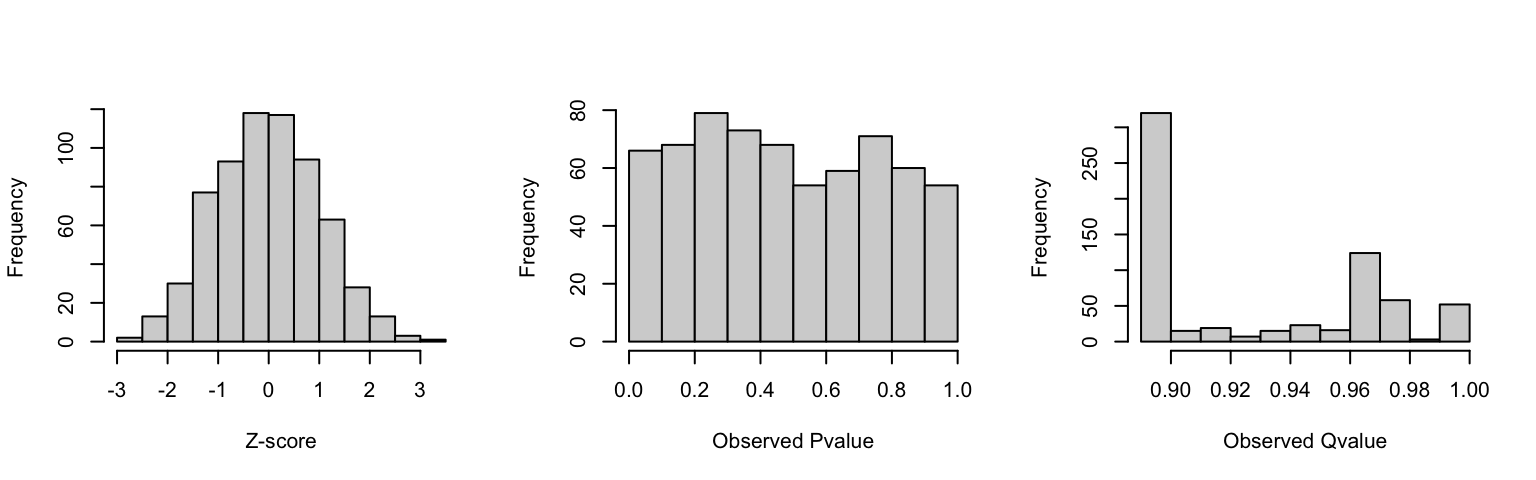

Estimating your experiment power

Another usufull application of decal simulation suite is conducting a power analysis to decide how much should you sequence or to define your tests filters. In the example below, we generated an experiment using sim_experiment_from_data which generates a random count matrix, a clone assignment list, and a perturbation table. The generated count matrix is based on your experiment matrix with the same dimensions, similar cells total count and gene average expression. The clone list is composed of 100 clones with 5 to 20 cells each. Perturbation table indicates pairs of clone and genes and the log2 fold-change applied, where for each clone a gene was randomly to apply a effect indicated by lfc. In this case, for each clone, 180 genes were selected and listed in pwr_dat$perturbations and among them 20 were perturbed by a log2 fold-change of -2, -1, 1, and 2.

pwr_lfc <- c(rep(c(-2, -1, 1, 2), each = 20), rep(0, 100))
pwr_dat <- sim_experiment_from_data(
  count, lfc = pwr_lfc, nclones = 100, min_n = 5, max_n = 20
)
pwr_res <- decal(pwr_dat$perturbations, pwr_dat$count, pwr_dat$clone)
pwr_res <- subset(pwr_res, !is.na(pvalue))

Adminitting a 5% FDR, we can estimated the ratio of the truly perturbated gene and clone pairs were detected by decal (left plot) and the clone size frequency (right plot). For all log2 fold-change applied here, decal obtained a power close to 80% that indicate que performance of the model.

par(mfrow = c(1, 2))
barplot(
  sapply(split(
    pwr_res$p_adjusted[pwr_res$expected_lfc != 0] < 0.05,
    pwr_res$expected_lfc[pwr_res$expected_lfc != 0]
  ), mean),
  xlab = "LFC", ylab = "Power")
abline(h = 0.8, lty = 2, col = "firebrick")
hist(sapply(pwr_dat$clone, length), main = "", xlab = "Number of perturbed cells")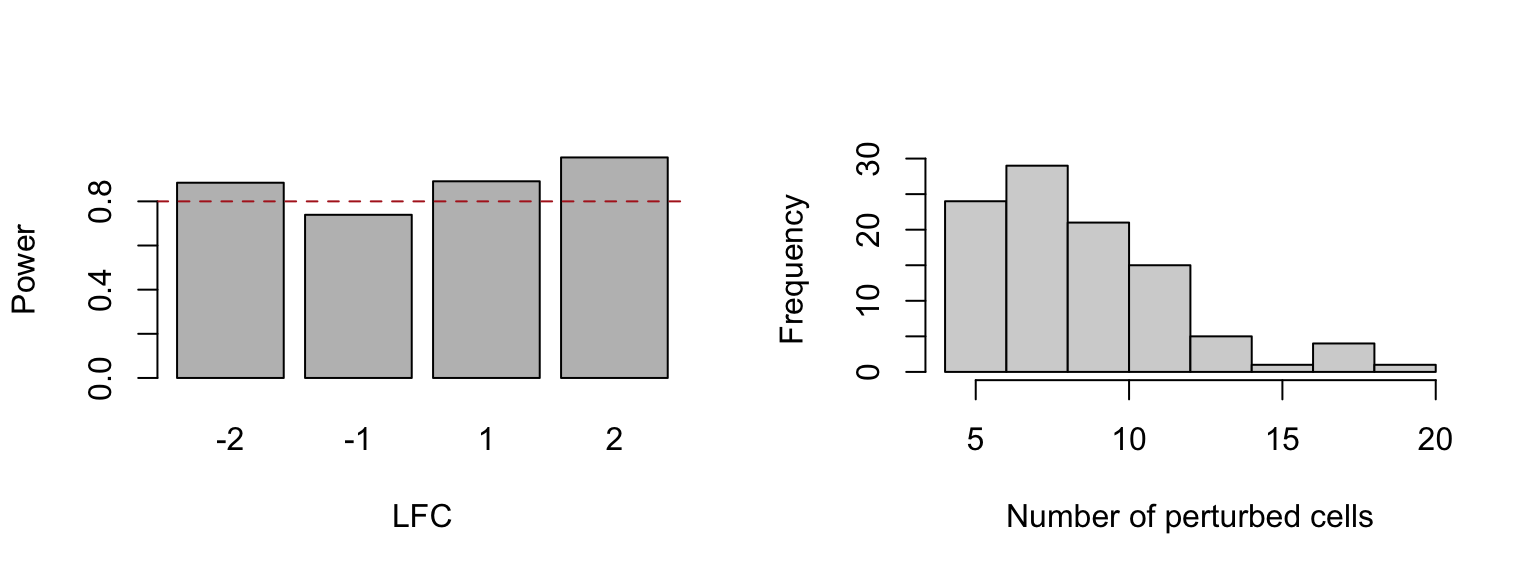

References

Ahlmann-Eltze, Constantin, and Wolfgang Huber. 2021. “glmGamPoi: Fitting Gamma-Poisson Generalized Linear Models on Single Cell Count Data.” Bioinformatics (Oxford, England) 36 (24): 5701–2. https://doi.org/10.1093/bioinformatics/btaa1009.

Anders, Simon, and Wolfgang Huber. 2010. “Differential Expression Analysis for Sequence Count Data.” Genome Biology 11 (10): R106. https://doi.org/10.1186/gb-2010-11-10-r106.

Hafemeister, Christoph, and Rahul Satija. 2019. “Normalization and Variance Stabilization of Single-Cell RNA-Seq Data Using Regularized Negative Binomial Regression.” Genome Biology 20 (1): 296. https://doi.org/10.1186/s13059-019-1874-1.

Love, Michael I., Wolfgang Huber, and Simon Anders. 2014. “Moderated Estimation of Fold Change and Dispersion for RNA-Seq Data with DESeq2.” Genome Biology 15 (12): 550. https://doi.org/10.1186/s13059-014-0550-8.

McCarthy, Davis J., Yunshun Chen, and Gordon K. Smyth. 2012. “Differential Expression Analysis of Multifactor RNA-Seq Experiments with Respect to Biological Variation.” Nucleic Acids Research 40 (10): 4288–97. https://doi.org/10.1093/nar/gks042.

Robinson, Mark D., Davis J. McCarthy, and Gordon K. Smyth. 2010. “edgeR: A Bioconductor Package for Differential Expression Analysis of Digital Gene Expression Data.” Bioinformatics (Oxford, England) 26 (1): 139–40. https://doi.org/10.1093/bioinformatics/btp616.

Svensson, Valentine. 2020. “Droplet scRNA-Seq Is Not Zero-Inflated.” Nature Biotechnology 38 (2): 147–50. https://doi.org/10.1038/s41587-019-0379-5.

Townes, F. William, Stephanie C. Hicks, Martin J. Aryee, and Rafael A. Irizarry. 2019. “Feature Selection and Dimension Reduction for Single-Cell RNA-Seq Based on a Multinomial Model.” Genome Biology 20 (1): 295. https://doi.org/10.1186/s13059-019-1861-6.

Session info

sessionInfo()
#> R version 4.1.2 (2021-11-01)
#> Platform: x86_64-apple-darwin17.0 (64-bit)
#> Running under: macOS Catalina 10.15.7
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib
#> 
#> locale:
#> [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] decal_0.1.1
#> 
#> loaded via a namespace (and not attached):
#>  [1] Rcpp_1.0.7      bookdown_0.24   lattice_0.20-45 digest_0.6.28  
#>  [5] MASS_7.3-54     grid_4.1.2      magrittr_2.0.1  evaluate_0.14  
#>  [9] highr_0.9       rlang_0.4.12    stringi_1.7.5   jquerylib_0.1.4
#> [13] Matrix_1.3-4    rmarkdown_2.11  tools_4.1.2     stringr_1.4.0  
#> [17] xfun_0.28       yaml_2.2.1      fastmap_1.1.0   compiler_4.1.2 
#> [21] fastglm_0.0.1   htmltools_0.5.2 knitr_1.36